Definition piecewise function
Table of Contents
Table of Contents
Have you ever struggled with drawing piecewise functions? Are you tired of not knowing how to accurately graph them? If so, you are not alone. Drawing piecewise functions can be a challenge for many people, but it doesn’t have to be. In this article, we will cover the basics of how to draw piecewise functions.
When it comes to drawing piecewise functions, many people struggle with knowing where to start. They may also find it difficult to graph different sections of the function properly. Additionally, people may not know how to handle specific scenarios, such as when a piecewise function contains absolute values or when the function has gaps.
To draw a piecewise function, start by looking at what the function is made up of. A piecewise function is simply a function that is defined by multiple equations, each corresponding to a different interval. Once you have identified these equations and their corresponding intervals, you can graph each part of the function separately.
Overall, the process of drawing piecewise functions can be broken down into a few basic steps:
- Identify the separate portions of the function.
- Determine the interval of each portion.
- Graph each portion of the function separately.
- Plot the holes, breaks, and/or other points of interest in the function.
With these steps in mind, let’s explore how to draw piecewise functions in more detail. Understanding Piecewise Functions
Piecewise functions can be tricky to handle. It is essential to have a solid understanding of the underlying concepts before proceeding. A piecewise function is a function that is defined by multiple equations for different parts of its domain. In other words, the function contains different expressions depending on the input value. The intervals at which the function transitions from one expression to another are called the breakpoints.
To draw a piecewise function, you must first identify the breakpoints and the corresponding expressions. Once you have determined the function’s different expressions, you can graph each portion of the function separately.
As you can see in the image above, the breakpoints are labeled on the graph. These are the points where the function transitions from one expression to another.
Common Piecewise Functions
There are several types of piecewise functions that you may encounter. One of the most common types is the absolute value function, which is written as f(x) = |x|. Graphing this function requires slightly different techniques, as the function is not continuous.
Another common type of piecewise function is the greatest integer function, which is written as f(x) = [x]. This function returns the largest integer less than or equal to x. When graphing this function, it is crucial to identify the breakpoints and understand how the function behaves at each breakpoint.
Graphing Piecewise Functions with Breaks and Holes
When graphing piecewise functions, you may encounter scenarios where the function has breaks or holes. A break occurs when there is a discontinuity in the function; a hole occurs when there is a missing point in the graph.
For instance, let’s say we have a piecewise function written as f(x) = x + 2 if x 1. In this function, there is a hole at x = 1, and the value of the function is undefined at this point. You should plot the point, but leave it as an open circle to indicate the hole.
The Importance of Practice
Like any new skill, drawing piecewise functions takes time and practice. It may seem overwhelming at first, but with regular practice, it can become more manageable. Start with basic piecewise functions and then progress to more complex ones. Use online resources to find practice problems and examples to develop your skills further.
Q&A: Common Questions about Drawing Piecewise Functions
Question 1: What type of functions can be expressed as piecewise functions?
Any function that has multiple expressions depending on the input value can be expressed as a piecewise function.
Question 2: Can you graph absolute value functions using the steps outlined in this article?
Yes, but you will need to follow slightly different techniques, as the function is not continuous.
Question 3: What do we do when a piecewise function has a gap?
A gap can occur when there is no defined expression for a particular interval. When this happens, you should leave a gap between the two portions of the function.
Question 4: How do you check your work when drawing piecewise functions?
You can check your work by verifying that each portion of the function lines up with the corresponding equation, that the breakpoints are accurate, and that any gaps or holes are appropriately labeled.
Conclusion of How to Draw Piecewise Functions
While drawing piecewise functions can be challenging, it is a skill that can be learned with practice. By following the steps outlined in this article, you can have greater confidence in your ability to graph piecewise functions accurately. Remember to start with simple piecewise functions and gradually work your way up to more complex ones. With time and practice, you’ll become a master of graphing piecewise functions.
Gallery
Piecewise Functions: Algebra - Math Lessons
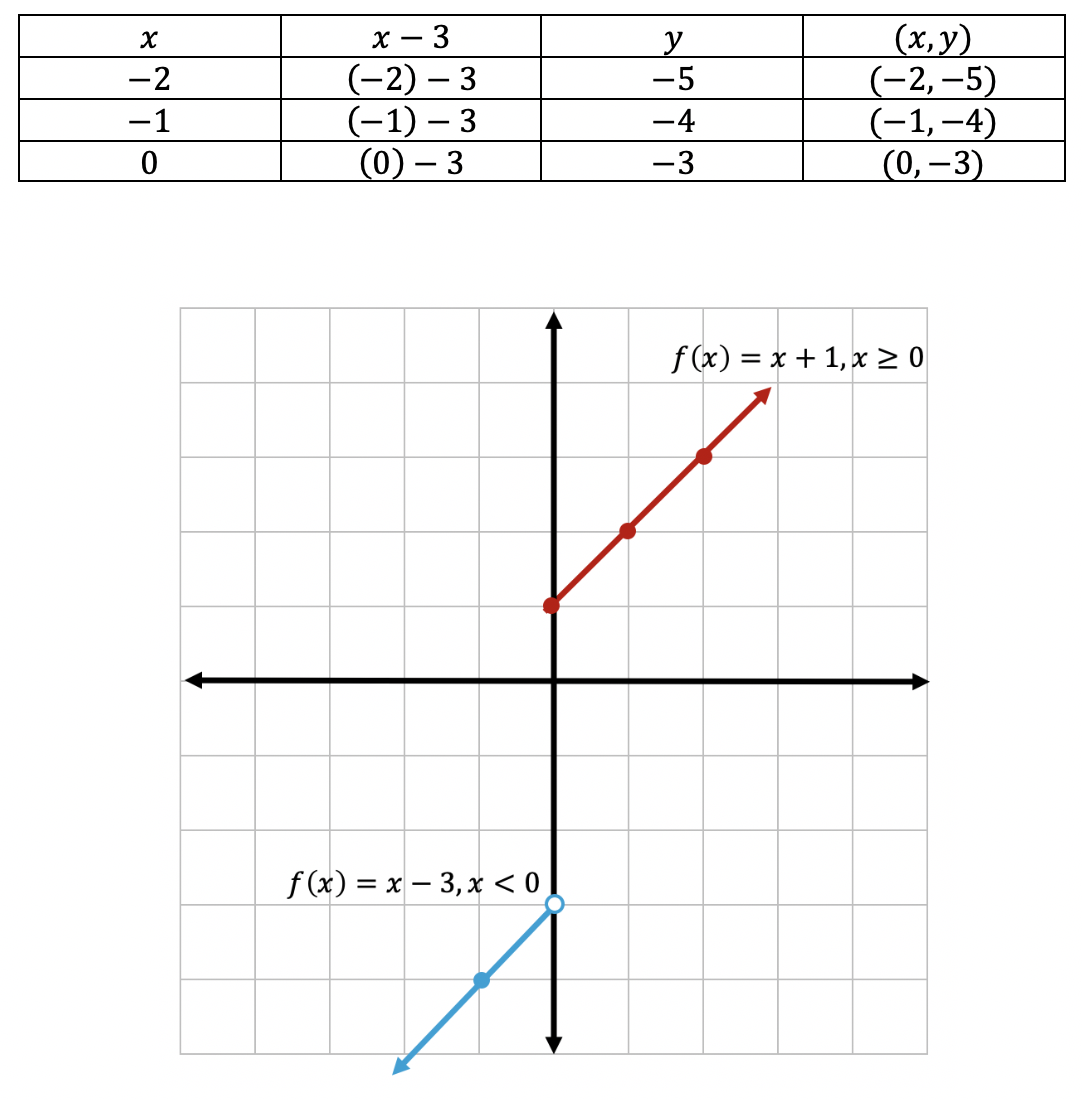
Photo Credit by: bing.com / piecewise functions algebra mathsux
Definition Piecewise Function - Holdenala
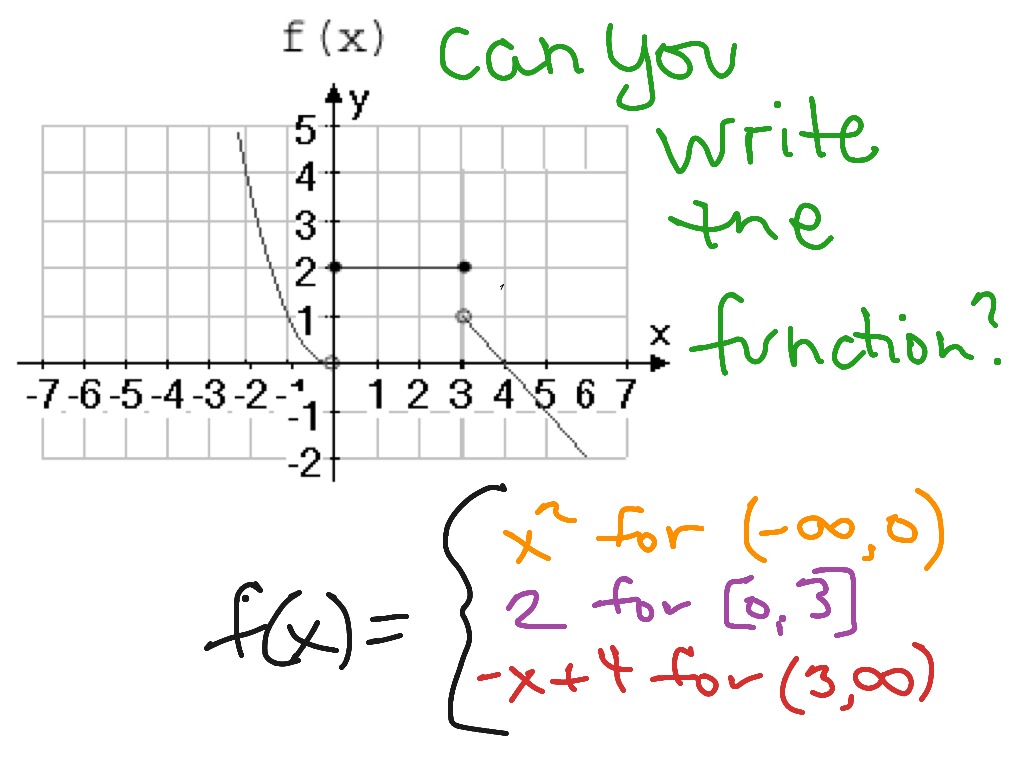
Photo Credit by: bing.com /
Piecewise Functions | Math | ShowMe
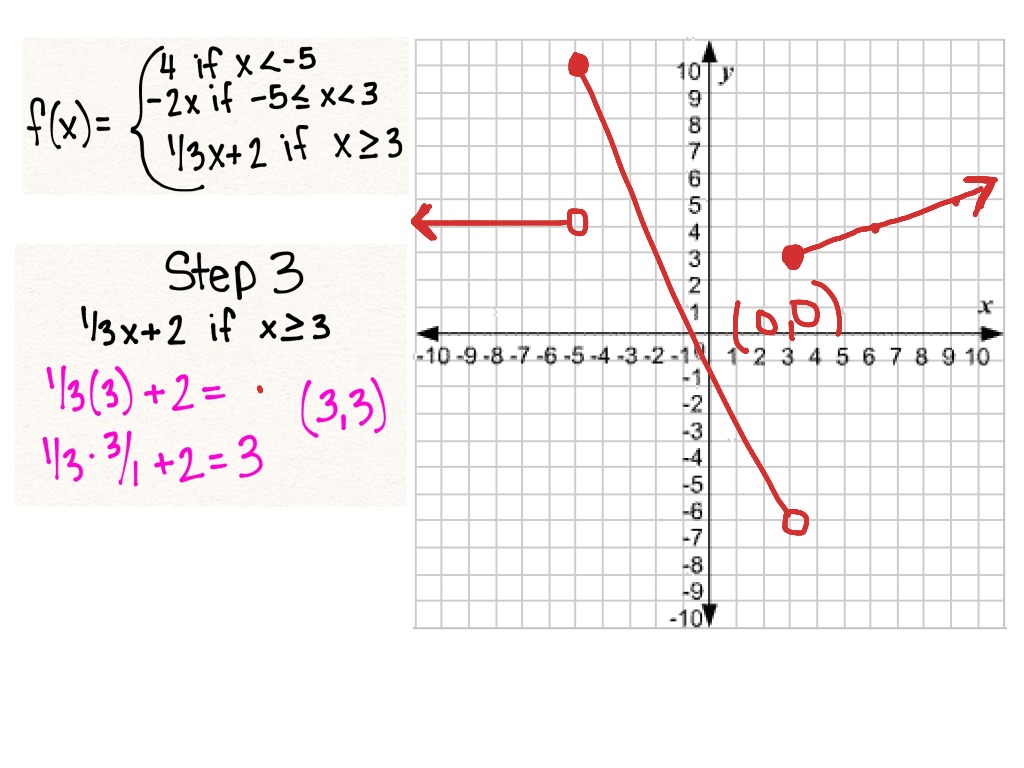
Photo Credit by: bing.com / piecewise
Piecewise Functions Equation Examples - Get Images
Photo Credit by: bing.com / piecewise equation ck
Which Piecewise Function Is Shown In The Graph? - Brainly.com
Photo Credit by: bing.com / piecewise function graph which shown brainly
