Draw the function given graph of derivative
Table of Contents
Table of Contents
If you are a student, you might be struggling to draw the first derivative graph. This is a common pain point for many students who are studying calculus. Drawing the first derivative graph can be challenging, but with the right techniques, you can master it.
When it comes to drawing the first derivative graph, students often face difficulties in identifying the critical points, inflection points, and concavity. These concepts can be confusing, but once you understand them, you will be able to draw the graph with ease.
The key to drawing the first derivative graph is to understand the relationship between the function and its derivative. The derivative of a function gives you the slope of the function at any given point. The slope of a function is the rate at which it changes.
To draw the first derivative graph, follow these steps:
- Identify the critical points of the function.
- Determine the sign of the derivative on each interval.
- Identify the inflection points of the function.
- Determine the concavity of the function on each interval.
- Draw the first derivative graph using the information obtained in the previous steps.
In summary, understanding the relationship between the function and its derivative is crucial in drawing the first derivative graph. By following the steps outlined above, you can draw the graph with ease.
How to Draw First Derivative Graph: My Personal Experience
When I first started learning how to draw the first derivative graph, I struggled to understand the concept of critical points and inflection points. However, with the help of my teacher and some online resources, I was able to grasp the concept.
One technique that I found helpful was to plot the original function first and then use the information obtained from the derivative to draw the first derivative graph. This helped me to visualize the relationship between the function and its derivative.
Another technique that I found helpful was to practice drawing the first derivative graph for different functions. The more I practiced, the more comfortable I became with the process.
The Relationship between the First Derivative Graph and the Original Function
The first derivative graph can give you a lot of information about the original function. By identifying the critical points and inflection points, you can determine the maximum and minimum values of the function. The concavity of the function can also be determined by looking at the first derivative graph.
Another useful piece of information that can be obtained from the first derivative graph is the location of the horizontal tangent lines. These lines occur when the derivative of the function is equal to zero.
Identifying Critical Points and Inflection Points
The critical points of the function are the points where the derivative is equal to zero or undefined. To find these points, you need to solve the derivative for x.
The inflection points of the function are the points where the concavity changes. To find these points, you need to take the second derivative of the function and set it equal to zero.
Determining Concavity
The concavity of the function can be determined by looking at the sign of the second derivative. If the second derivative is positive, the function is concave up. If the second derivative is negative, the function is concave down.
Tips for Drawing the First Derivative Graph
Here are some tips to help you draw the first derivative graph:
- Label the x and y-axes.
- Use different colors to differentiate the positive and negative portions of the graph.
- Draw the horizontal tangent lines as dotted lines to differentiate them from the rest of the graph.
- Clearly label the critical points and inflection points.
Question and Answer
Q: What is the first derivative of a function?
A: The first derivative of a function gives you the slope of the function at any given point.
Q: What is the relationship between the first derivative graph and the original function?
A: The first derivative graph can give you a lot of information about the original function. By identifying the critical points and inflection points, you can determine the maximum and minimum values of the function. The concavity of the function can also be determined by looking at the first derivative graph.
Q: What are the critical points of a function?
A: The critical points of a function are the points where the derivative is equal to zero or undefined.
Q: Why is it important to understand the first derivative graph?
A: The first derivative graph is an essential tool in analyzing the behavior of functions. By understanding the first derivative graph, you can determine the maximum and minimum values of the function, locate the inflection points, and determine the concavity of the function.
Conclusion of How to Draw First Derivative Graph
Drawing the first derivative graph can be challenging, but with the right techniques, you can master it. Understanding the relationship between the function and its derivative is crucial to drawing the first derivative graph. By following the steps outlined in this article, you can draw the graph with ease. Remember to practice drawing the first derivative graph for different functions to become more comfortable with the process. With practice, you will be able to draw the first derivative graph quickly and accurately.
Gallery
Derivative Graph Vs Original Function (w/ 15+ Examples!)
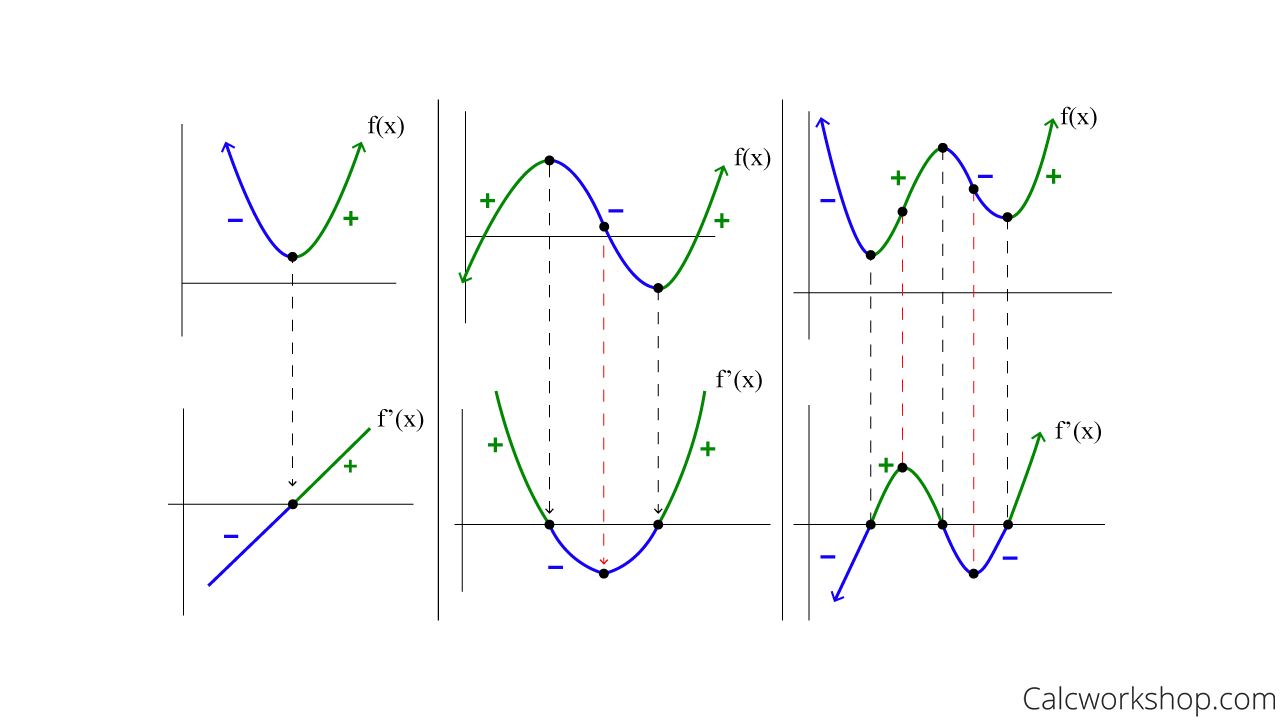
Photo Credit by: bing.com / derivative
How To Sketch First Derivative And Function From Graph Of Second

Photo Credit by: bing.com / derivative graph second function sketch
Sketching Derivative Graphs At PaintingValley.com | Explore Collection
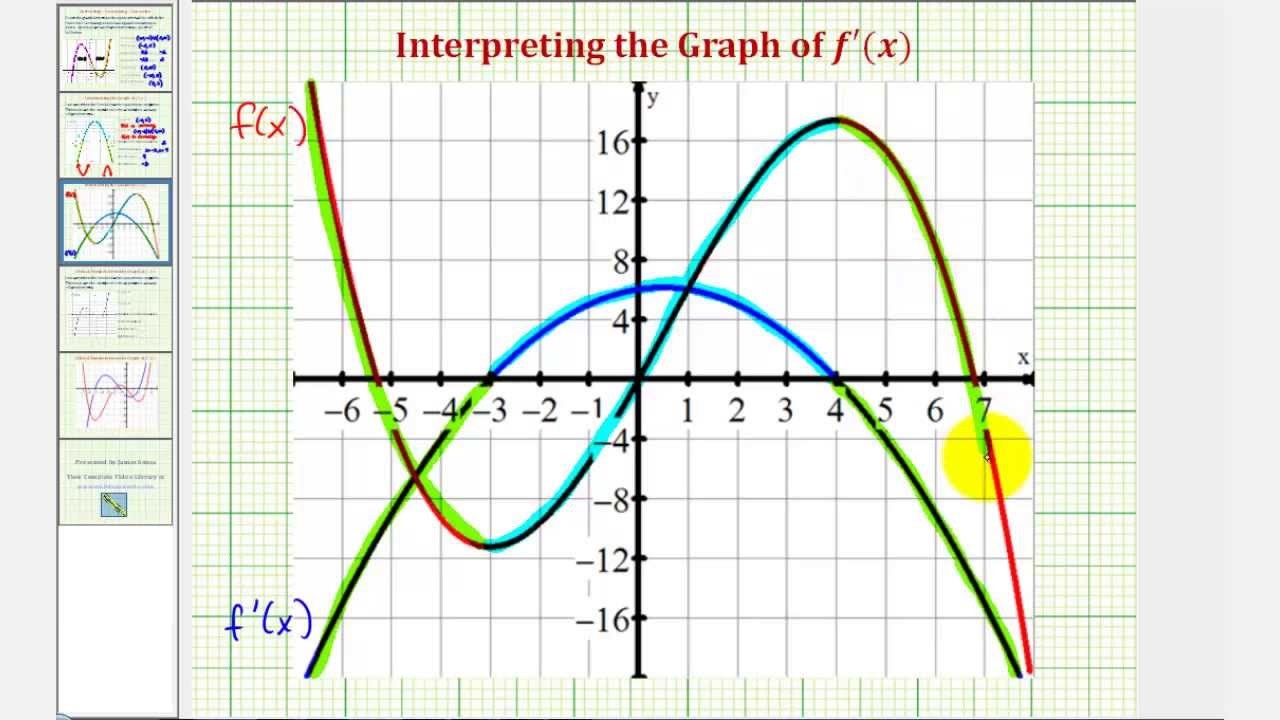
Photo Credit by: bing.com / derivative graphs sketching graph function interpret paintingvalley ex
Draw The Function Given Graph Of Derivative - YouTube

Photo Credit by: bing.com / derivative graph function draw given
Derivative Graph Vs Original Function (w/ 15+ Examples!)
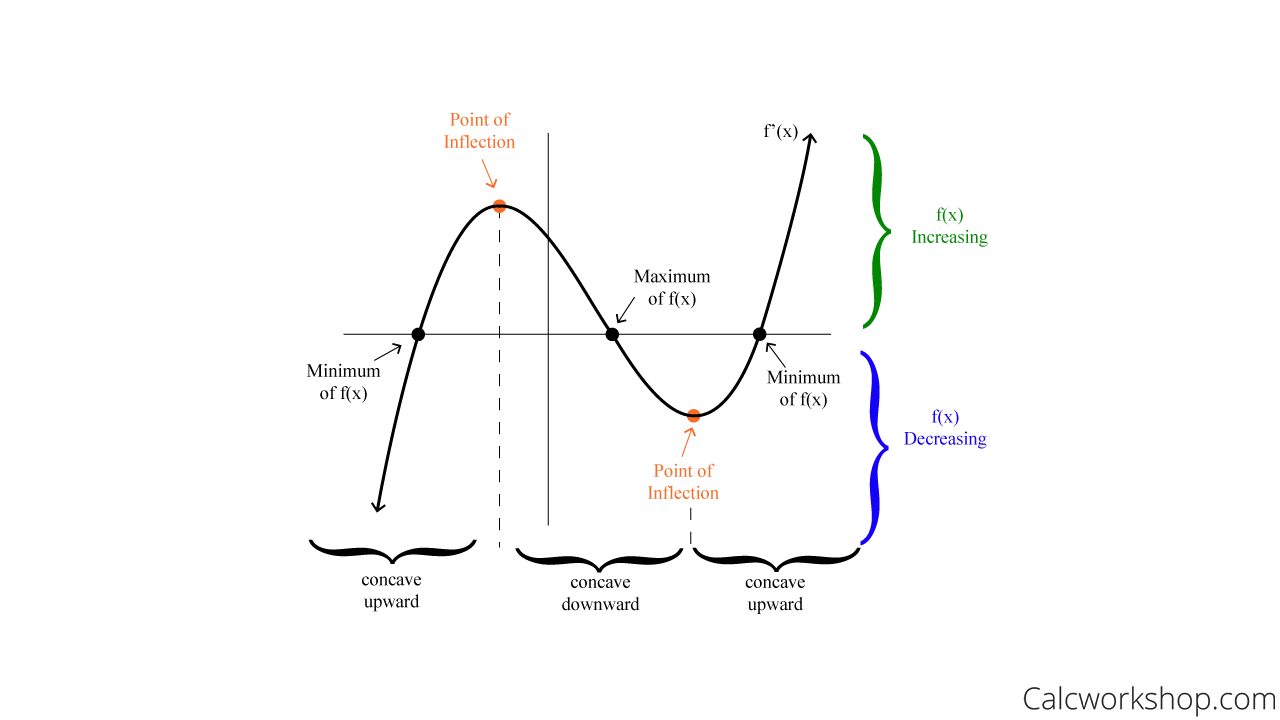
Photo Credit by: bing.com / derivative






